유클리드 호제법이란?
유클리드 알고리즘 (Euclidean algorithm)은 2개의 자연수의 최대공약수(GCD) 를 구하는 알고리즘입니다. 해당 알고리즘에 대해서 조금 자세하게 이야기 해보겠습니다.
다음과 같은 조건을 가정합니다.
1. A != B
2. A > B
만약 ( A )와 ( B )가 같다면, 최대공약수는 ( A ) 또는 ( B ) 중 어느 것을 사용해도 동일합니다. 조건에서 ( A > B )라고 명시했지만, 이는 두 수의 순서가 중요하지 않다는 것을 의미합니다. 예를 들어, (12, 3)과 (3, 12)와 같이 두 수의 순서가 바뀌어도 최대공약수는 변하지 않습니다. 즉, 유클리드 호제법은 일반성을 잃지 않고 항상 유효하게 작동합니다.
유클리드 호제법의 기본 원리는 다음과 같습니다: 두 수 ( A )와 ( B )에 대해, ( A )를 ( B )로 나눈 나머지를 ( r ) 몫을 ( a )라고 할 때, 다음과 같은 식이 성립됩니다. (증명은 너무 수학 이야기라서 궁금하신 분은 한 번 찾아보세요 ㅎㅎ)
A = aB + r, gcd(A, B) = gcd(B, r) = gcd(r, r1) = gcd(r1, r2) .... gcd (x, 0) x가 최대 공약수
수학적인 Tip
0 <= r < B < A
어디서 많이 본 수식 아닌가요?? 바로 재귀 함수입니다. 즉, 유클리드 호제법 이론을 응용하면 재귀 함수로 두 자연수의 최대 공약수를 구할 수 있습니다.
재귀 함수
private int getGCD(int A, int B) {
// B가 0이면 A가 최대공약수
if (B == 0) {
return A;
}
// gcd(A, B) = (B, r1) ... gcd(x, 0) x가 최대 공약수라고 인지하면 해당 재귀함수를 이해하기 쉬움
return getGCD(B, A % B);
}B가 '0'면 A가 최대 공약수라고 위에 코드에 명시했는데 여기에는 '0'의 비밀 때문에 성립됩니다. '0'의 약수는 뭘까요?? 바로 모든 정수입니다. 왜 그런지 간단하게 설명하면 모든 정수의 배수에는 '0'이 속해있기 때문입니다.
재귀함수로 최대공약수를 구할 수 있으니 당연히 반복문으로도 최대 공약수를 구할 수 있습니다.
반복문
// 해당 코드를 보기전에 gcd(A, B) = gcd(B, r)이 성립된다는 걸 보고 아래 코드를 보면 이해가 쉽습니다
private int getGCD(int a, int b) {
while (b != 0) { // ... gcd(x, 0) 이니 b가 0이 아닐 때 까지 반복
int temp = b; // b값을 미리 temp에 저장
b = a % b; // b를 나머지(r)로 변경
a = temp; // 미리 저장한 b를 a로 변경
}
return a;
}
최소 공배수
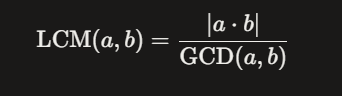
유클리드 호재법으로 최대 공약수 gcd(a, b)를 구할 수 있죠?? 이제 미지수가 한 개 되므로 최소 공배수를 구할 수 있습니다. 코드로 보면
private int getLCD(int a, int b){
return Math.abs(a * b) / getGCD(a, b);
}※ 너무 수학적인 이론이라서 자세한 설명은 안하겠습니다.
'알고리즘 > 이론' 카테고리의 다른 글
| Stack, Queue에 peek()메소드 차이점 (0) | 2025.03.22 |
|---|---|
| [Java] 자바 자료구조 간단 정리 - 코테용 (0) | 2025.02.14 |
| 시간 복잡도, 공간 복잡도, 빅오 표기법 간단 정리 (0) | 2025.02.11 |

